数字图像处理之图像特征检测

发表于 | 分类于 ， | 阅读次数：
本文字数： 8.2k | 阅读时长 ≈ 7 分钟

实验要求

  1. 边缘检测
  2. 霍夫线变换
  3. 霍夫圆变换

算法实现

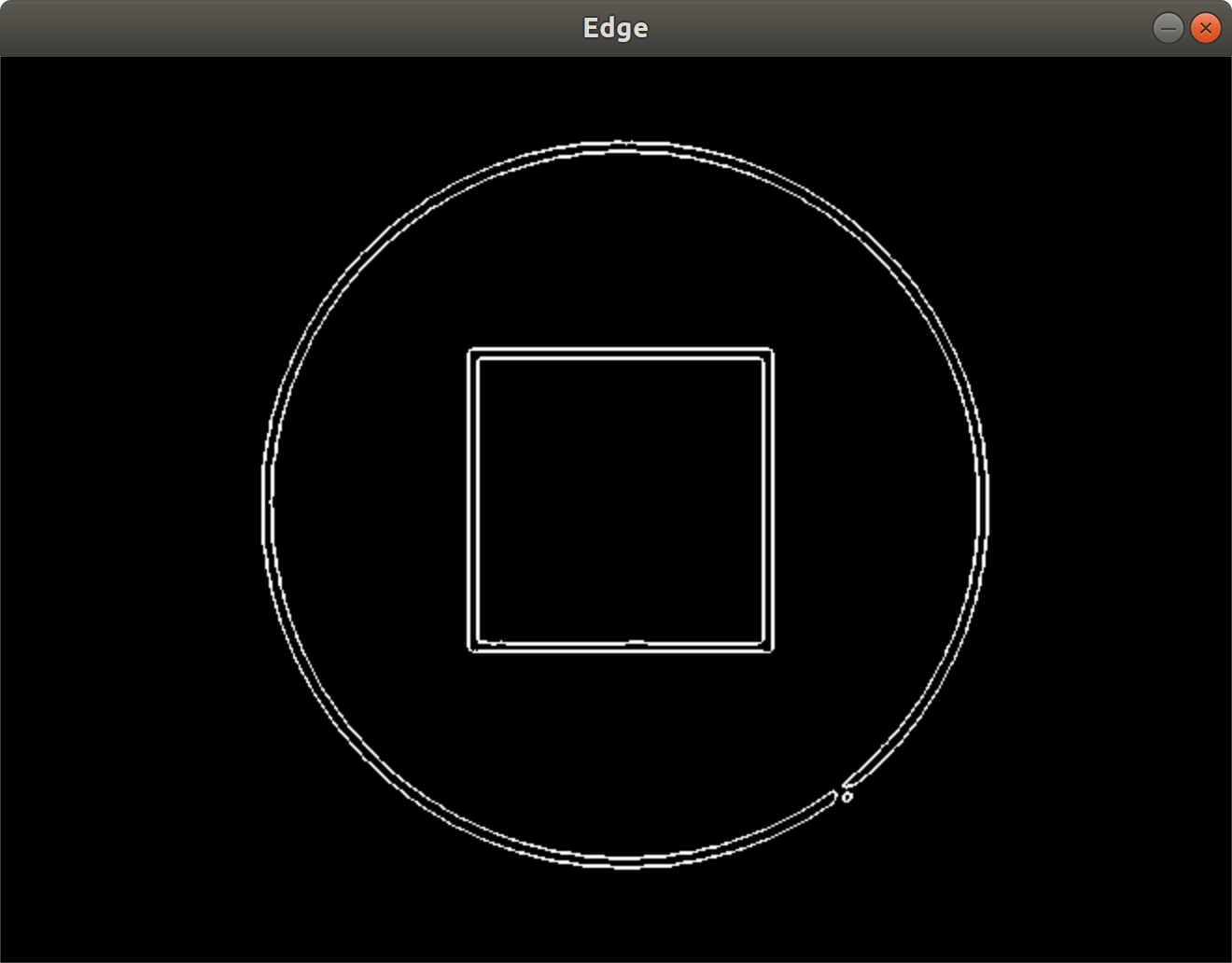
边缘检测

本代码采用LoG边缘检测算子

  1. 算子与图像卷积
  2. 寻找零交叉点，即边缘点

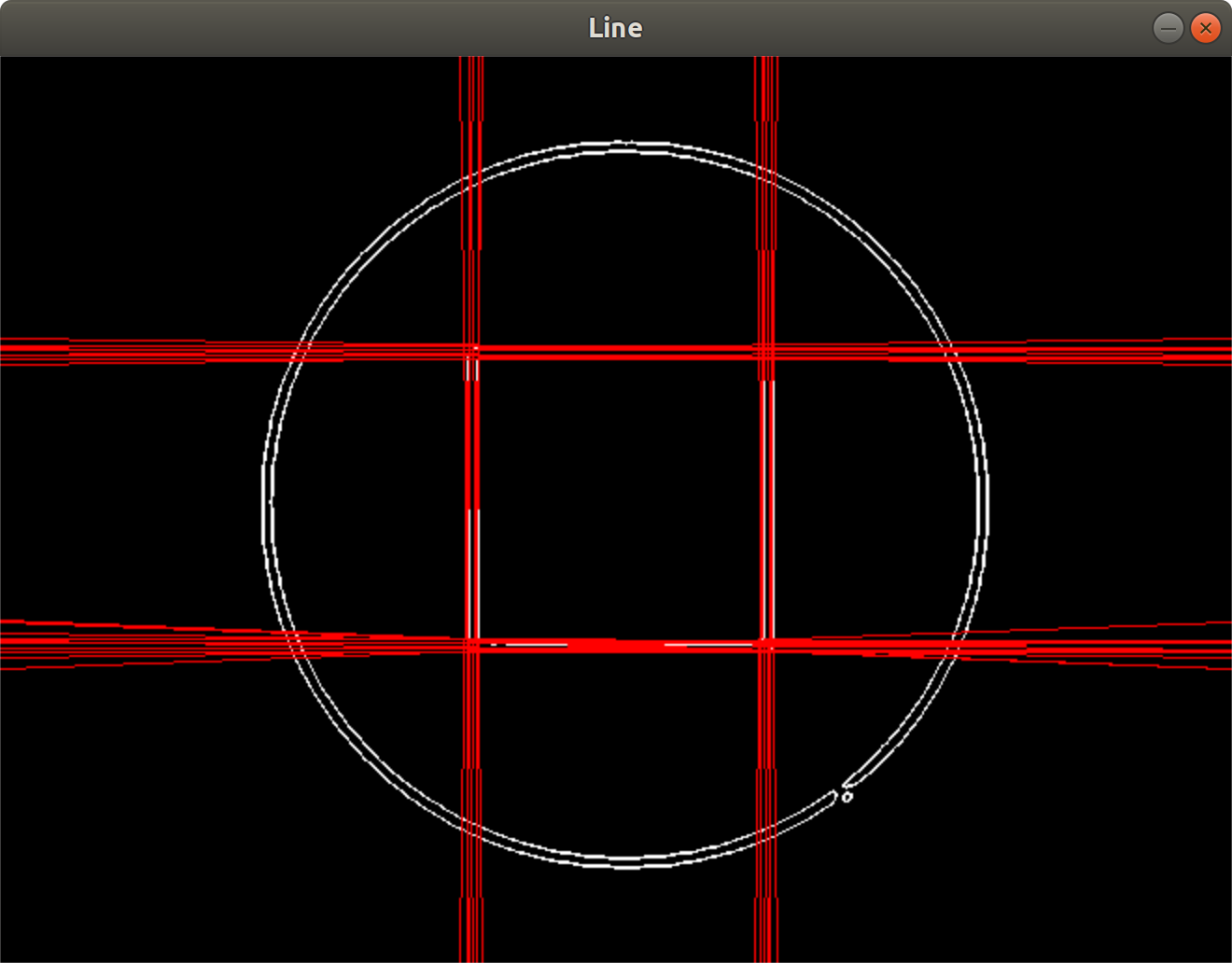
霍夫线变换

  1. 将彩色图像转化为灰度图，并对灰度图做边缘检测得到二值边缘图

  2. 参数空间离散化:对直线方程的参数$(r,\theta)$离散化，并给出$(r_{min},r_{max})$和$(\theta_{min},\theta_{max})$，划分为有限个等间距的离散值，使参数空间量化为一个个等大小网格。

  3. 设置累加器A:为每个网格单元设置累加器。A表示$(r_{min}:r_{max},\theta_{min}:\theta_{max})$，初始为0。

  4. 对图像空间中每个像素点坐标值(x,y)，计算参数空间对应的曲线方程，将该曲线穿过的格子的计数值加一。

  5. 最后，遍历A(i,j)中的寻找累加计数大于某阈值M格子，其坐标$(r_m, \theta_m)$即为检测到的直线参数。利用cvtColor()将二值边缘图转换为RGB图，并将检测到的所有直线在图中画出来。

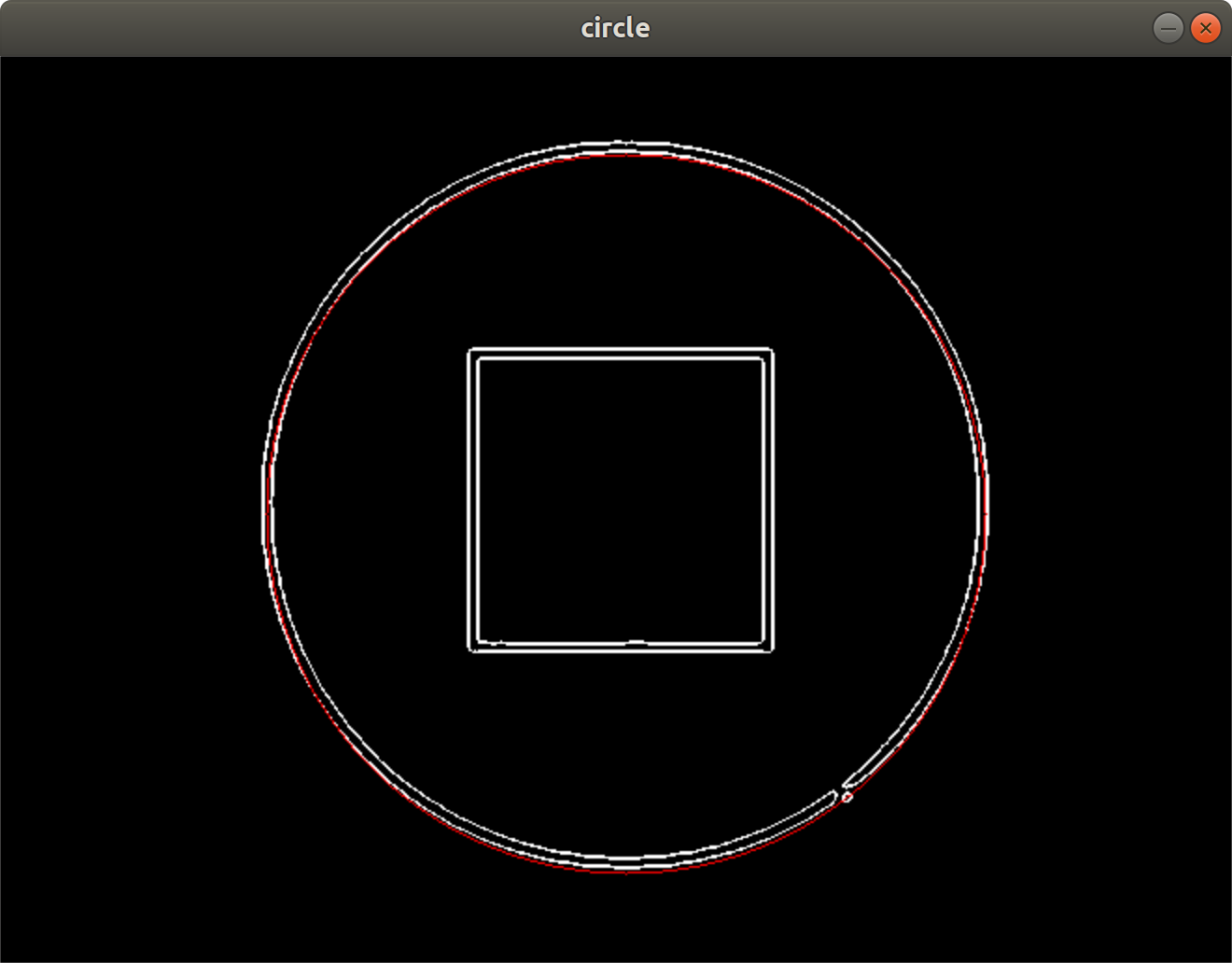
霍夫圆变换

  1. 将彩色图像转化为灰度图，并对灰度图做边缘检测得到二值边缘图

  2. 设定检测半径和角度范围$(r_{min}:r_{max},\theta_{min}:\theta_{max})$，ax)，设置累加器A(x,y,r)

  3. 对图像空间中每个像素点坐标值(x,y)，在指定半径和圆心角范围内，计算参数空间对应的圆心，累加器A(x_center, y_center,r)加一。

  4. 最后，遍历累加器中的寻找累加计数大于某阈值M格子，其坐标$(x_center, y_center,r)$即为检测到的圆参数。利用cvtColor()将二值边缘图转换为RGB图，并将检测到的所有直线在图中画出来。

显然这样的方法效率很低，时间和空间复杂度都很高，所以我们用梯度法优化。

  1. 用sobel算子计算出整张图的梯度

  2. 对于图像中每个点，在其梯度方向上的点的累加器A(x,y)加一

  3. 遍历A(i,j)中的寻找累加计数大于某阈值M格子，其坐标$(x,y)$即为可能是圆心的点。

  4. 对于每个圆心计算每个像素点与他的距离，并塞入数组R，然后寻找最多的半径R的数量，如果大于阈值那么就以该圆心半径画圆。若俩个圆心距离很近，那么就选其一。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
#include <stdlib.h>
#include <opencv2/opencv.hpp>
#include <opencv2/core/core.hpp>
#include <vector>
#define LINEAR_X 0

#define SIZE 5
#define PI 3.1415926
#define oo 1e9+7
#define theta_cnt 500
using namespace cv;
using namespace std;
//////////////////////边缘检测//////////////////
//边缘检测函数 LoG边缘检测算子
void EdgeDetector(Mat input, Mat &output){
	threshold(input, input, 150, 255, THRESH_BINARY);
	//imshow("threshold",input);
 	double Gaussian_Temp[SIZE][SIZE] = {{0,0,-1,0,0},
					{0,-1,-2,-1,0},
					{-1,-2,16,-2,-1},
					{0,-1,-2,-1,0},
					{0,0,-1,0,0}};//模板
	//Mat Temp=Mat::zeros(input.size(),CV_8UC1);

	int rows = input.rows;
	int cols = input.cols;
	double *Temp  = new double[rows*cols];
	for(int i=0;i<rows;i++)
	{
		for(int j=0;j<cols;j++)
		{
			double sum = 0;
			for(int k=0;k<SIZE;k++)
				for(int t=0;t<SIZE;t++)
				{
					int x=i+k-SIZE/2;
					int y=j+t-SIZE/2;
					if(x<0||y<0||x>=rows||y>=cols)continue;
					double m=Gaussian_Temp[k][t];
					sum+=m*input.at<uchar>(x,y);
					
				}
			Temp[i*cols+j]=sum;
		}
	}
	
	//寻找零交叉
	int dx[2][4]={{-1,0,1,-1},//上，左，左上，左下
			{1,0,-1,1}};//下，右，右下，右上
	int dy[2][4]={{0,-1,-1,-1},//上，左，左上，左下
			{0,1,1,1}};//下，右，右下，右上
	for(int i=0;i<rows;i++)
	{
		for(int j=0;j<cols;j++)
		{
			int pa,pb,num=0;
			for(int k=0;k<4;k++){
				int x1=i+dx[0][k],y1=j+dy[0][k];
				int x2=i+dx[1][k],y2=j+dy[1][k];
				if(x1<0||y1<0||x1>=rows||y1>=cols)pa=0;
				else pa=Temp[x1*cols+y1];
				if(x2<0||y2<0||x2>=rows||y2>=cols)pb=0;
				else pb=Temp[x2*cols+y2];
				if(pa*pb<0&&abs(pa-pb)>255*0.5)num++;
				//cout<<pa<<" "<<pb<<endl;
			}
			if(num>=2)output.at<uchar>(i,j)=255;
			else output.at<uchar>(i,j)=0;
		}
	}
}
//////////////////////霍夫线变换//////////////////
Mat Hough_Line(Mat input){
	Mat output=Mat::zeros(input.size(),CV_8UC3);
	cvtColor(input,output,COLOR_GRAY2BGR);
	int rows = input.rows;
	int cols = input.cols;
	int max_length = sqrt(pow(rows,2)+pow(cols,2));
	int r_cnt=max_length*2;	
	int M = 100;//阈值
	int *A = new int[r_cnt*theta_cnt];//累加器
	//遍历，并累加
	for(int i=0;i<rows;i++)
	{
		for(int j=0;j<cols;j++)
		{
			if(input.at<uchar>(i,j)==0)continue;
			for(int k=0;k<theta_cnt;k++){
				double theta=2.0*PI*k/theta_cnt;
				int r=1.0*i*cos(theta)+1.0*j*sin(theta);//直线方程
				if(r<-max_length||r>=max_length)continue;
				A[(r+max_length)*theta_cnt+k]++;
			}
		}
	}
	//画直线
	for(int i=0;i<r_cnt;i++){
		for(int j=0;j<theta_cnt;j++){
			if(A[i*theta_cnt+j]<M)continue;
			if((i>0&&A[i*theta_cnt+j]<A[(i-1)*theta_cnt+j])
				||(j>0&&A[i*theta_cnt+j]<A[i*theta_cnt+j-1]))continue;
			if((i<r_cnt-1&&A[i*theta_cnt+j]<A[(i+1)*theta_cnt+j])
				||(j<theta_cnt-1&&A[i*theta_cnt+j]<A[i*theta_cnt+j+1]))continue;
			double theta=2.0*PI*j/theta_cnt;
			int r = i-max_length;
			double a = cos(theta);
			double b = sin(theta);
			double x1 = int(b*r + 1000*(a));
			double y1 = int(a*r + 1000*(-b));
			double x2 = int(b*r - 1000*(a));
			double y2 = int(a*r - 1000*(-b));
			line(output,Point(x1,y1),Point(x2,y2),Scalar(0,0,255),1);

		}
	}
	return output;
}
//////////////////////霍夫圆变换//////////////////
Mat calc(Mat input,double kernel[3][3],int Size){
	Mat output=Mat::zeros(input.size(),CV_8UC1);
	int rows = input.rows;
	int cols = input.cols;
	for(int i=0;i<rows;i++)
	{
		for(int j=0;j<cols;j++)
		{
			for(int k=0;k<Size;k++)
				for(int t=0;t<Size;t++)
				{
					int x=i+k-Size/2;
					int y=j+t-Size/2;
					if(x<0||y<0||x>=rows||y>=cols)continue;
					double m=kernel[k][t];
					output.at<int>(i,j)+=m*input.at<uchar>(x,y);
				}
		}
	}
	return output;
}
Mat Hough_Circle(Mat input){
	Mat output=Mat::zeros(input.size(),CV_8UC3);
	cvtColor(input,output,COLOR_GRAY2BGR);
	int rows = input.rows;
	int cols = input.cols;
	int r_max=max(rows,cols)/2;	
	double M = 0.1;
	int A[rows][cols]={0};

	double sobelx[3][3]={{1,2,1},
			 {0,0,0},
			 {-1,-2,-1}};
	double sobely[3][3]={{1,0,-1},
			 {2,0,-2},
			 {1,0,-1}};

	Mat dx=calc(input,sobelx,3);
	Mat dy=calc(input,sobely,3);
	//累加器寻找圆心
	for(int i=0;i<rows;i++)
	{ 
		for(int j=0;j<cols;j++)
		{
			if(input.at<uchar>(i,j)==0)continue;
			double vx=dx.at<int>(i,j);
			double vy=dy.at<int>(i,j);
			double mag=sqrt(vx*vx+vy*vy);
			if(mag == 0)continue;
			double sx=vx/mag;
			double sy=vy/mag;
			for(int t=-1;t<2;t+=2){
				double x=1.0*i+sx*t;
				double y=1.0*j+sy*t;
				for(int r=0;r<r_max;r++,x+=sx*t,y+=sy*t)
				{
					int X=int(x),Y=int(y);
					if(X<0||Y<0||X>=rows||Y>=cols)break;
					A[X][Y]++;
				}
			}
		}
	}
	//寻找可能圆心
	vector<Point>centerP;
	vector<Point>circleP;
	for(int i=0;i<rows;i++)
	{
		for(int j=0;j<cols;j++)
		{
			if(A[i][j]<50)continue;
			if((i>0&&A[i][j]<A[i-1][j])||(j>0&&A[i][j]<A[i][j-1]))continue;
			if((i<rows-1&&A[i][j]<A[i+1][j])||(j<cols-1&&A[i][j]<A[i][j+1]))continue;
			centerP.push_back(Point(i,j));
		}
	}
	//对每个可能圆心，寻找可能半径
	int l=centerP.size();
	for(int i=0;i<l;i++){
		int cx=centerP[i].x;
		int cy=centerP[i].y;
		int L=circleP.size();
		bool flag=0;
		for(int j=0;j<L;j++){
			int cx1=circleP[j].x;
			int cy1=circleP[j].y;
			 if( pow(( cx1- cx),2) + pow( cy1- cy,2) <= 9){//圆心相近
				flag=1;
                break;
			}
		}
		if(flag)continue;
		
		vector<int>R;
		for(int k=0;k<rows;k++)
		{
			for(int t=0;t<cols;t++)
			{
				if(input.at<uchar>(k,t)==0)continue;
				int r=sqrt(pow(cx-k,2)+pow(cy-t,2));
				if(r+cx<rows&&r+cy<cols&&cx-r>=0&&cy-r>=0)R.push_back(r);
			}
		}
		//半径数最多的就是最有可能的
		if(R.size()==0)continue;
		sort(R.begin(),R.end());
		int startR=R[0],cnt=0,maxcnt=0,ansR=0;
		for(int j=1;j<R.size();j++){
			int r=R[j];
			if(r-startR>2){
				int nowR=(R[j-1]+startR)/2;
				if(cnt*ansR>=maxcnt*nowR){
					ansR=nowR;
					maxcnt=cnt;
				}
				cnt=0;
				startR=r;
			}
			cnt++;
		}
		if(maxcnt>700){
			circle(output, Point(cy,cx),ansR , Scalar(0, 0, 255), 0.5);	
			circleP.push_back(Point(cx,cy));
		}
	}/**/
	return output;
}
int main(int argc,char **argv){
	//读取原始图像
	Mat src=imread(argv[1],IMREAD_UNCHANGED);
	//检查是否读取图像
	if(src.empty()){
		std::cout<<"Error! Input image cannot be read...\n";
		return -1;
	}
	
	imshow("src",src);
	
	// 灰度图转换
	Mat garyimg;
	cvtColor(src,garyimg,COLOR_BGR2GRAY);
	imshow("gray",garyimg);  

	// 边缘检测函数
	Mat frOut1=Mat::zeros(garyimg.size(),CV_8UC1);
	EdgeDetector(garyimg, frOut1);
	// 线检测
	Mat frOut2=Hough_Line(frOut1);
	// 圆检测
	Mat frOut3=Hough_Circle(frOut1) ;

	imshow("Edge",frOut1);
	imshow("Line",frOut2);
	imshow("circle",frOut3);
	std::cout << "Press any key to exit...\n";
    waitKey(); // Wait for key press
	return 0;
}

运行结果

原图
原图
原图
原图